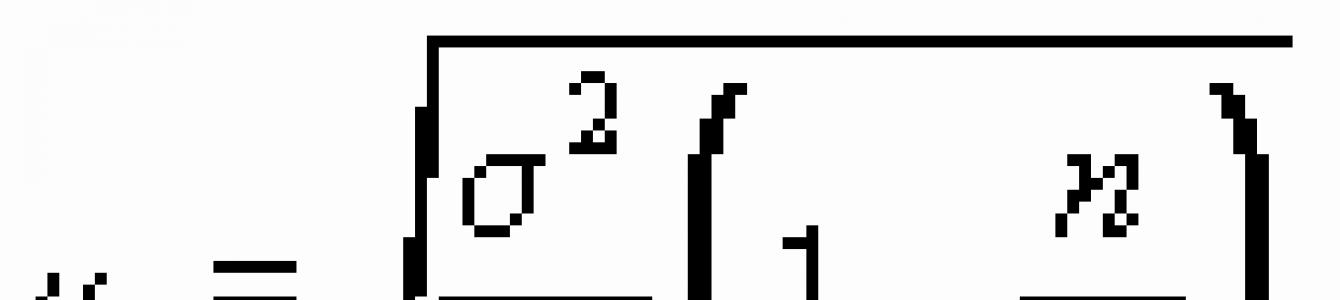Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n ), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику - среднюю ошибку выборки () .
В теории выборочного наблюдения выведены формулы для определения , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то определяется как:
При оценивании среднего значения признака;
Если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 - n/N):
 - для среднего значения признака;
- для среднего значения признака;
 - для доли.
- для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки () равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае - двойной средней ошибки) - 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 - практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше - по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
В рассматриваемом примере имеем 40%-ную выборку (90: 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., x i | количество предприятий, f i | середина интервала, x i \xb4 | x i \xb4 f i | x i \xb4 2 f i |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | - | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60: 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N 1 + N 2 + … + N i + … + N k = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n 1 + n 2 + … + n i + … + n k = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = n i · N i /N
где n i - количество извлекаемых единиц для выборки из i-й типической группы;
n - общий объем выборки;
N i - количество единиц генеральной совокупности, составивших i-ю типическую группу;
N - общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Здесь - средняя из групповых дисперсий типических групп.
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., N i | Обследовано в результате выборочного наблюдения, чел., n i | Среднее число посещений библиотеки одним студентом за семестр, x i | Внутригрупповая выборочная дисперсия, |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | - |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
аналогично для других групп:
![]()
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения - распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Ошибка выборки - это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.
Для репрезентативности выборки важно обеспечить случайность отбора, с тем, чтобы все объекты генеральной совокупности имели равные вероятности попасть в выборку. Для обеспечения репрезентативности выборки применяют следующие способы отбора:
· собственно-случайная (простая случайная) выборка (последовательно отбирается первый случайно попавшийся объект);
· механическая (систематическая) выборка;
· типическая (стратифицированная, расслоенная) выборка (объекты отбираются пропорционально представительству различных типов объектов в генеральной совокупности);
· серийная (гнездовая) выборка.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным. При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует
Выборочное наблюдение всегда связано с ошибкой, поскольку число отобранных единиц не равно исходной (генеральной) совокупности. Случайные ошибки выборки обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Поэтому получаемые случайные ошибки должны быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка таких ошибок и является основной задачей, решаемой в теории выборочного наблюдения. Обратной задачей является определение такой минимально необходимой численности выборочной совокупности, при которой ошибка не превысит заданной величины. На выработку навыков в решении этих задач и направлен материал данного раздела.
Собственно-случайная выборка . Ее суть заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков.
После проведения отбора с использованием одного из алгоритмов, реализующих принцип случайности, или на основе таблицы случайных чисел, определяются границы генеральных характеристик. Для этого рассчитываются средняя и предельная ошибки выборки.
Средняя ошибка повторной собственно-случайной выборки определяется по формуле
где σ - среднее квадратическое отклонение изучаемого признака;
n - объем (число единиц) выборочной совокупности.
Предельная ошибка выборки связана с заданным уровнем вероятности. При решении представленных ниже задач требуемая вероятность составляет 0,954 (t = 2) или 0,997 (t = 3). С учетом выбранного уровня вероятности и соответствующего ему значения t предельная ошибка выборки составит:
Тогда можно утверждать, что при заданной вероятности генеральная средняя будет находиться в следующих границах:
![]()
При определении границ генеральной доли при расчете средней ошибки выборки используется дисперсия альтернативного признака, которая вычисляется по следующей формуле:
![]()
где w - выборочная доля, т. е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака.
При решении отдельных задач необходимо учитывать, что при неизвестной дисперсии альтернативного признака можно использовать ее максимально возможную величину, равную 0,25.
Пример . В результате выборочного обследования незанятого населения, ищущего работу, проведенного на основе собственно-случайной повторной выборки были получены данные, приведенные в табл. 1.14.
Таблица 1.14
Результаты выборочного обследования незанятого населения
С вероятностью 0,954 определите границы:
а) среднего возраста незанятого населения;
б) доли (удельного веса) лиц, моложе 25 лет, в общей численности незанятого населения.
Решение. Для определения средней ошибки выборки необходимо, прежде всего, определить выборочную среднюю величину и дисперсию изучаемого признака. Для этого, при ручном способе расчета целесообразно построить таблицу 1.15.
Таблица 1.15
Расчет среднего возраста незанятого населения и дисперсии
На основании данных таблицы рассчитываются необходимые показатели:
· выборочная средняя величина:
![]() ;
;
· дисперсия:
![]()
· среднеквадратичное отклонение:
![]() .
.
Средняя ошибка выборки составит:
![]() года.
года.
Определим с вероятностью 0,954 (t = 2) предельную ошибку выборки:
![]() года.
года.
Установим границы генеральной средней: (41,2 - 1,6) (41,2+1,6) или:
Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний возраст незанятого населения, ищущего работу, лежит в пределах от 40 до 43 лет.
Для ответа на вопрос, поставленный в пункте «б» данного примера, по выборочным данным определим долю лиц в возрасте до 25 лет и рассчитаем дисперсию доли:
![]()
Рассчитаем среднюю ошибку выборки:
![]()
Предельная ошибка выборки с заданной вероятностью составит:
![]()
Определим границы генеральной доли:
![]()
Следовательно, с вероятностью 0,954 можно утверждать, что доля лиц в возрасте до 25 лет в общей численности незанятого населения находится в пределах от 3,9 до 1 1,9%.
При расчете средней ошибки собственно-случайной бесповторной выборки необходимо учитывать поправку на бесповторность отбора:

где N - объем (число единиц) генеральной совокупности/
Необходимый объем собственно-случайной повторной выборки определяется по формуле:
Если отбор бесповторный, то формула приобретает следующий вид:

Полученный на основе использования этих формул результат всегда округляется в большую сторону до целого значения.
Пример. Необходимо определить, сколько учащихся первых классов школ района необходимо отобрать в порядке собственно-случайной бесповторной выборки, чтобы с вероятностью 0,997 определить границы среднего роста первоклассников с предельной ошибкой 2 см. Известно, что всего в первых классах школ района обучается 1100 учеников, а дисперсия роста по результатам аналогичного обследования в другом районе составила 24.
Решение. Необходимый объем выборки при уровне вероятности 0,997 (t = 3) составит:
![]()
Таким образом, для получения данных о среднем росте первоклассников с заданной точностью необходимо обследовать 52 школьника.
Механическая выборка . Данная выборка заключается в отборе единиц из общего списка единиц генеральной совокупности через равные интервалы в соответствии с установленным процентом отбора. При решении задач на определение средней ошибки механической выборки, а также необходимой ее численности, следует использовать приведенные выше формулы, применяемые при собственно-случайном бесповторном отборе.
Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке - каждая 20-я единица (1:0,05) и т.д.
Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т.д.
Типическая выборка. Эта выборка применяется в тех случаях, когда единицы генеральной совокупности объединены в несколько крупных типичных групп. Отбор единиц в выборку производится внутри этих групп пропорционально их объему на основе использования собственно-случайной или механической выборки (при наличии необходимой информации отбор также может производиться пропорционально вариации изучаемого признака в группах).
Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации.
Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
Средняя ошибка типической выборки определяется по формулам:
(повторный отбор);
![]() (бесповторный отбор),
(бесповторный отбор),
где - средняя из внутригрупповых дисперсией.
Пример . В целях изучения доходов населения по трем районам области сформирована 2%-ная выборка, пропорциональная численности населения этих районов. Полученные результаты представлены в табл. 16.
Таблица 16
Результаты выборочного обследования доходов населения
Необходимо определить границы среднедушевых доходов населения по области в целом при уровне вероятности 0,997.
Решение. Рассчитаем среднюю из внутригрупповых дисперсий:
где N i - объем i -и группы;
n, - объем выборки из /-и группы.
Серийная выборка . Эта выборка используется в тех случаях, когда единицы изучаемой совокупности объединены в небольшие равновеликие группы или серии. Единицей отбора в этом случае является серия. Серии отбираются с использованием собственно-случайной либо механической выборки, а внутри отобранных серий обследуются все без исключения единицы.
В основе расчета средней ошибки серийной выборки лежит межгрупповая дисперсия:
(повторный отбор);
![]() (бесповторный отбор),
(бесповторный отбор),
где x i - число отобранных i - серий;
R - общее число серий.
Межгрупповую дисперсию при равновеликих группах вычисляют следующим образом:
![]()
где х i - средняя i-и серии;
х - общая средняя по всей выборочной совокупности.
Пример . В целях контроля качества комплектующих из партии изделий, упакованных в 50 ящиков по 20 изделий в каждом, была произведена 10%-ная серийная выборка. По попавшим в выборку ящикам среднее отклонение параметров изделия от нормы соответственно составило 9 мм, 11, 12, 8 и 14 мм. С вероятностью 0,954 определите среднее отклонение параметров по всей партии в целом.
Решение. Выборочная средняя:
![]() мм.
мм.
Величина межгрупповой дисперсии:
С учетом установленной вероятности Р = 0,954 (t = 2) предельная ошибка выборки составит:
![]() мм.
мм.
Произведенные расчеты позволяют заключить, что среднее отклонение параметров всех изделий от нормы находится в следующих границах:
Для определения необходимого объема серийной выборки при заданной предельной ошибке используются следующие формулы:
(повторный отбор);
![]() (безповторный отбор).
(безповторный отбор).
Представляет из себя такое расхождение между средними выборочной и генеральной совокупностями, которое не превышает ±б (дельта).
На основании теоремы Чебышева П. Л. величина средней ошибки при случайном повторном отборе рассчитывается по формуле (для среднего количественного признака):
где числитель - дисперсия признака х в выборочной совокупности;
n - численность выборочной совокупности.
Для альтернативного признака формула средней ошибки выборки для доли по теореме Я. Бернулли рассчитывается по формуле:

где р(1- р) - дисперсия доли признака в генеральной совокупности;
n - объем выборки.
Вследствие, того что дисперсия признака в генеральной совокупности точно не известна, на практике используют значение дисперсии, которое рассчитано для выборочной совокупности на основании закона больших чисел . Согласно данному закону выборочная совокупность при большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Поэтому расчетные формулы средней ошибки при случайном повторном отборе будут выглядеть таким образом:
1. Для среднего количественного признака:

где S^2 - дисперсия признака х в выборочной совокупности;
n - объем выборки.

где w (1 — w) - дисперсия доли изучаемого признака в выборочной совокупности.
В теории вероятностей было показано, что выражается через выборочную согласно формуле:
![]()
В случаях малой выборки , когда её объем меньше 30, необходимо учитывать коэффициент n/(n-1). Тогда среднюю ошибку малой выборки рассчитывают по формуле:

Так как в процессе бесповторной выборки сокращается численность единиц генеральной совокупности, то в представленных выше формулах расчета средних ошибок выборки нужно подкоренное выражение умножить на 1- (n/N).
Расчетные формулы для такого вида выборки будут выглядеть так:
1. Для средней количественного признака:
где N - объем генеральной совокупности; n - объем выборки.
2. Для доли (альтернативного признака):

где 1- (n/N) — доля единиц генеральной совокупности, не попавших в выборку.
Поскольку n всегда меньше N, то дополнительный множитель 1 — (n/N) всегда будет меньше единицы. Это означает, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. Когда доля единиц генеральной совокупности, которые не попали в выборку, существенная, то величина 1 — (n/N) близка к единице и тогда расчет средней ошибки производится по общей формуле.
Средняя ошибка зависит от следующих факторов:
1. При выполнении принципа случайного отбора средняя ошибка выборки определяется во-первых объемом выборки: чем больше численность, тем меньше величины средней ошибки выборки . Генеральная совокупность характеризуется точнее тогда, когда больше единиц данной совокупности охватывает выборочное наблюдение
2. Средняя ошибка также зависит от степени варьирования признака. Степень варьирования характеризуется . Чем меньше вариация признака (дисперсия), тем меньше средняя ошибка выборки. При нулевой дисперсии (признак не варьируется) средняя ошибка выборки равна нулю, таким образом, любая единица генеральной совокупности будет характеризовать всю совокупность по этому признаку.
При выборочном наблюдении должна быть обеспечена слу-чайность отбора единиц. Каждая единица должна иметь равную с другими возможность быть отобранной. Именно на этом основывается собственно-случайная выборка.
К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности (без предварительного рас-членения ее на какие-либо группы) посредством жеребьевки (преимущественно) или какого-либо иного подобного спосо-ба, например, с помощью таблицы случайных чисел. Случай-ный отбор -- это отбор не беспорядочный. Принцип случай-ности предполагает, что на включение или исключение объ-екта из выборки не может повлиять какой-либо фактор, кро-ме случая. Примером собственно-случайного отбора могут служить тиражи выигрышей: из общего количества выпущен-ных билетов наугад отбирается определенная часть номеров, на которые приходятся выигрыши. Причем всем номерам обеспечивается равная возможность попадания в выборку. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля выборки есть отношение числа единиц выборочной со-вокупности к числу единиц генеральной совокупности:
Так, при 5%-ной выборке из партии деталей в 1000 ед. объ-ём выборки п составляет 50 ед., а при 10%-ной выборке -- 100 ед. и т.д. При правильной научной организации выборки ошибки репрезентативности можно свести к минимальным значениям, в результате -- выборочное наблюдение становится достаточно точным.
Собственно-случайный отбор «в чистом виде» применяет-ся в практике выборочного наблюдения редко, но он является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного наблюдения.
Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.
Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателей: среднюю величину ко-личественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются от всех других единиц этой сово-купности только наличием изучаемого признака).
Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п:
Например, если из 100 деталей выборки (n =100), 95 деталей оказались стандартными (т =95), то выборочная доля
w =95/100=0,95 .
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.
Ошибка выборки ? или, иначе говоря, ошибка репрезента-тивности представляет собой разность соответствующих выбо-рочных и генеральных характеристик:
*
*
Ошибка выборки свойственна только выборочным наблюде-ниям. Чем больше значение этой ошибки, тем в большей степе-ни выборочные показатели отличаются от соответствующих генеральных показателей.
Выборочная средняя и выборочная доля по своей сути яв-ляются случайными величинами, которые могут принимать раз-личные значения в зависимости от того, какие единицы сово-купности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возмож-ных ошибок -- среднюю ошибку выборки.
От чего зависит средняя ошибка выборки? При соблюдении принципа случайного отбора средняя ошибка выборки определя-ется прежде всего объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, всё более точно характеризуем всю генеральную совокупность.
Средняя ошибка выборки также зависит от степени варьи-рования изучаемого признака. Степень варьирования, как из-вестно, характеризуется дисперсией? 2 или w(1-w) -- для альтернативного признака. Чем меньше вариация признака, а следовательно, и дисперсия, тем меньше средняя ошибка вы-борки, и наоборот. При нулевой дисперсии (признак не варь-ирует) средняя ошибка выборки равна нулю, т. е. любая еди-ница генеральной совокупности будет совершенно точно ха-рактеризовать всю совокупность по этому признаку.
Зависимость средней ошибки выборки от ее объема и степе-ни варьирования признака отражена в формулах, с помощью которых можно рассчитать среднюю ошибку выборки в условиях выборочного наблюдения, когда генеральные характеристики (х,p) неизвестны, и следовательно, не представляется возмож-ным нахождение реальной ошибки выборки непосредственно по формулам (форм. 1), (форм. 2).
Ш При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:
* для средней количественного признака
* для доли (альтернативного признака)
Поскольку практически дисперсия признака в генеральной совокупности? 2 точно неизвестна, на практике пользуются значением дисперсии S 2 , рассчитанным для выборочной сово-купности на основании закона больших чисел, согласно кото-рому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики гене-ральной совокупности.
Таким образом, расчетные формулы средней ошиб-ки выборки при случайном повторном отборе будут следующие:
* для средней количественного признака
* для доли (альтернативного признака)
Однако дисперсия выборочной совокупности не равна диспер-сии генеральной совокупности, и следовательно, средние ошибки выборки, рассчитанные по формулам (форм. 5) и (форм. 6), будут прибли-женными. Но в теории вероятностей доказано, что генеральная дисперсия выражается через выборную следующим соотношением:
Так как п/ (n -1) при достаточно больших п -- величина, близкая к единице, то можно принять, что, а следова-тельно, в практических расчетах средних ошибок выборки мож-но использовать формулы (форм. 5) и (форм. 6). И только в случаях ма-лой выборки (когда объем выборки не превышает 30) необхо-димо учитывать коэффициент п /(n -1) и исчислять среднюю ошибку малой выборки по формуле:
Ш X При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подко-ренное выражение умножить на 1-(n/N), поскольку в процес-се бесповторной выборки сокращается численность единиц генеральной совокупности. Следовательно, для бесповторной вы-борки расчетные формулы средней ошибки выборки примут такой вид:
* для средней количественного признака
* для доли (альтернативного признака)
. (форм. 10)
Так как п всегда меньше N , то дополнительный множи-тель 1-(n/N ) всегда будет меньше единицы. Отсюда следу-ет, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. В то же время при сравнительно небольшом проценте выборки этот множитель близок к еди-нице (например, при 5%-ной выборке он равен 0,95; при 2%-ной -- 0,98 и т.д.). Поэтому иногда на практике пользуются для определения средней ошибки выборки формулами (форм. 5) и (форм. 6) без указанного множителя, хотя выборку и организуют как бесповторную. Это имеет место в тех случаях, когда число единиц генеральной совокупности N неизвестно или безгра-нично, или когда п очень мало по сравнению с N , и по су-ществу, введение дополнительного множителя, близкого по значению к единице, практически не повлияет на значение средней ошибки выборки.
Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, разбитой по ней-тральному признаку на равные интервалы (группы), произво-дится таким образом, что из каждой такой группы в выборку отбирается лишь одна единица. Чтобы избежать систематиче-ской ошибки, отбираться должна единица, которая находится в середине каждой группы.
При организации механического отбора единицы совокуп-ности предварительно располагают (обычно в списке) в опре-деленном порядке (например, по алфавиту, местоположению, в порядке возрастания или убывания значений какого-либо по-казателя, не связанного с изучаемым свойством, и т.д.), после чего отбирают заданное число единиц механически, через оп-ределенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки. Так, при 2%-ной выборке отбирается и проверяется каждая 50-я единица (1: 0,02), при 5%-ной выборке -- каждая 20-я едини-ца (1: 0,05), например, сходящая со станка деталь.
При достаточно большой совокупности механический отбор по точности результатов близок к собственно-случайному. По-этому для определения средней ошибки механической выборки используют формулы собственно-случайной бесповторной вы-борки (форм. 9), (форм. 10).
Для отбора единиц из неоднородной совокупности применя-ется, так называемая типическая выборка , которая используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели.
При обследовании предприятий такими группами могут быть, например, отрасль и подотрасль, формы собственности. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении слож-ных статистических совокупностей. Например, при выборочном обследовании семейных бюджетов рабочих и служащих в отдель-ных отраслях экономики, производительности труда рабочих пред-приятия, представленных отдельными группами по квалификации.
Типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц в выбороч-ную совокупность. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представи-тельство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки.
При определении средней ошибки типической выборки в ка-честве показателя вариации выступает средняя из внутригрупповых дисперсий.
Среднюю ошибку выборки находят по формулам:
* для средней количественного признака
(повторный отбор); (форм. 11)

(бесповоротный отбор); (форм. 12)
* для доли (альтернативного признака)
(повторный отбор); (форм.13)
(бесповторный отбор), (форм. 14)
где - средняя из внутригрупповых дисперсий по вы-борочной совокупности;
Средняя из внутригрупповых дисперсий доли (альтернативного признака) по выборочной совокупности.
Серийная выборка предполагает случайный отбор из генераль-ной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий) с тем, чтобы в таких группах подвергать наблюде-нию все без исключения единицы.
Применение серийной выборки обусловлено тем, что многие товары для их транспортировки, хранения и продажи упаковываются в пачки, ящики и т.п. Поэтому при контроле качества упакованного товара рациональнее проверить не-сколько упаковок (серий), чем из всех упаковок отбирать необходимое количество товара.
Поскольку внутри групп (серий) обследуются все без исключе-ния единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.
Ш Среднюю ошибку выборки для средней количественного признака при серийном отборе находят по формулам:
(повторный отбор); (форм.15)
(бесповторный отбор), (форм. 16)
где r - число отобранных серий; R - общее число серий.
Межгрупповую дисперсию серийной выборки вычисляют сле-дующим образом:

где - средняя i - й серии; - общая средняя по всей выбо-рочной совокупности.
Ш Средняя ошибка выборки для доли (альтернативного при-знака) при серийном отборе:
(повторный отбор); (форм. 17)
(бесповторный отбор). (форм. 18)
Межгрупповую (межсерийную) дисперсию доли серийной вы-борки определяют по формуле:

, (форм. 19)
где - доля признака в i -й серии; - общая доля признака во всей выборочной совокупности.
В практике статистических обследований помимо рассмот-ренных ранее способов отбора применяется их комбинация (комбинированный отбор).
Средняя и предельная ошибки выборки
Основное преимущество выборочного наблюдения среди прочих других - возможность рассчитать случайную ошибку выборки.
Ошибки выборки бывают систематические и случайные.
Систематические - в том случае, когда нарушен основной принцип выборки - случайности. Случайные - возникают обычно ввиду того, что структура выборочной совокупности всегда отличается от структуры генеральной совокупности, как бы правильно ни был произведен отбор, то есть, несмотря на принцип случайности отбора единиц совокупности, все же имеются расхождения между характеристиками выборочной и генеральной совокупности. Изучение и измерение случайных ошибок репрезентативности и является основной задачей выборочного метода.
Как правило, чаще всего рассчитывают ошибку средней и ошибку доли. При расчетах используются следующие условные обозначения:
Средняя, рассчитанная в пределах генеральной совокупности;
Средняя, рассчитанная в пределах выборочной совокупности;
р - доля данной группы в генеральной совокупности;
w - доля данной группы в выборочной совокупности.
Используя условные обозначения, ошибки выборки для средней и для доли можно записать следующим образом:
Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать любые значения в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок μ.
В отличие от систематической, случайную ошибку можно определить заранее, до проведения выборки, согласно предельных теорем, рассматриваемых в математической статистике.
Средняя ошибка определяется с вероятностью 0,683. В случае другой вероятности говорят о предельной ошибке.
Средняя ошибка выборки для средней и для доли определяется следующим образом:
![]()
В этих формулах дисперсия признака является характеристикой генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными xapaктеристиками выборочной совокупности на основании закона больших чисел, по которому выборочная совокупность большом объеме точно воспроизводит характеристики генеральной совокупности.
Формулы определения средней ошибки для различных способ отбора:
| Способ отбора | Повторный | Бесповторный | ||
| ошибка средней | ошибка доли | ошибка средней | ошибка доли | |
| Собственно-случайный и механический | |
|||
| Типический | |
|||
| Серийный |
μ - средняя ошибка;
∆ - предельная ошибка;
п - численность выборки;
N - численность генеральной совокупности;
w - доля данной категории в общей численности выборки:
Средняя из внутригрупповых дисперсии;
Δ 2 - межгрупповая дисперсия;
r - число серий в выборке;
R - общее число серий.
Предельная ошибка для всех способов отбора связана со средней ошибкой выборки следующим образом:
где t - коэффициент доверия, функционально связанный с вероятностью, с которой обеспечивается величина предельной ошибки. В зависимости от вероятности коэффициент доверия t принимает следующие значения:
| t | P |
| 0,683 | |
| 1,5 | 0,866 |
| 2,0 | 0,954 |
| 2,5 | 0,988 |
| 3,0 | 0,997 |
| 4,0 | 0,9999 |
Например, вероятность ошибки равна 0,683. Это значит, что генеральная средняя отличается от выборочной средней по абсолютной величине не более чем на величину μ с вероятностью 0,683, то если - выборочная средняя, - генеральная средняя, то с вероятностью 0,683.
Если мы хотим обеспечить большую вероятность выводов, тем самым мы увеличиваем границы случайной ошибки.
Таким образом, величина предельной ошибки зависит от следующих величин:
Колеблемости признака (прямая связь), которую характеризует величина дисперсии;
Численности выборки (обратная связь);
Доверительной вероятности (прямая связь);
Метода отбора.
Пример расчета ошибки средней и ошибки доли.
Для определения среднего числа детей в семье методом случайной бесповторной выборки из 1000 семей отобраны 100. Результаты приведены в таблице:
Определите: .
- с вероятностью 0,997 предельную ошибку выборки и границы, в которых находится средне число детей в семье;
- с вероятностью 0,954 границы, в которых находится удельный вес семей с двумя детьми.
1. Определим предельную ошибку средней с вероятностью 0,977. Для упрощения расчетов воспользуемся способом моментов:
![]()

p = 0,997 t = 3
![]()
средняя ошибка средней, 0,116 - предельная ошибка
2,12 – 0,116 ≤ ≤ 2,12+ 0,116
2,004 ≤ ≤ 2,236
Следовательно, с вероятностью 0,997 среднее число детей в семье в генеральной совокупности, то есть среди 1000 семей, находится в интервале 2,004 - 2,236.